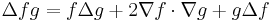Del in cylindrical and spherical coordinates

This is a list of some vector calculus formulae of general use in working with various curvilinear coordinate systems.

1 Note
2 References
3 See also
4 External links

Note

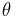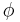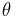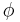This page uses standard physics notation. For spherical coordinates, $\theta$ is the angle between the z axis and the radius vector connecting the origin to the point in question. $\phi$ is the angle between the projection of the radius vector onto the x-y plane and the x axis. Some sources reverse the definitions of $\theta$ and $\phi$ , so the meaning should be inferred from the context.
The function atan2(y, x) can be used instead of the mathematical function arctan(y/x) due to its domain and image. The classical arctan(y/x) has an image of (-π/2, +π/2), whereas atan2(y, x) is defined to have an image of (-π, π]. (The expressions for the Del in spherical coordinates may need to be corrected)

**Table with the del operator in cylindrical, spherical and parabolic cylindrical coordinates**
Operation	Cartesian coordinates (x,y,z)	Cylindrical coordinates (ρ,φ,z)	Spherical coordinates (r,θ,φ)	Parabolic cylindrical coordinates (σ,τ,z)
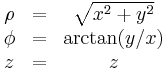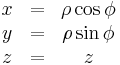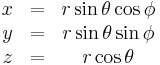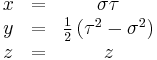Definition of coordinates	$\begin{matrix} \rho & = & \sqrt{x^2%2By^2} \\ \phi & = & \arctan(y/x) \\ z & = & z \end{matrix}$	$\begin{matrix} x & = & \rho\cos\phi \\ y & = & \rho\sin\phi \\ z & = & z \end{matrix}$	$\begin{matrix} x & = & r\sin\theta\cos\phi \\ y & = & r\sin\theta\sin\phi \\ z & = & r\cos\theta \end{matrix}$	$\begin{matrix} x & = & \sigma \tau\\ y & = & \frac{1}{2} \left( \tau^{2} - \sigma^{2} \right) \\ z & = & z \end{matrix}$
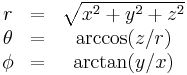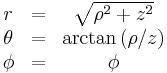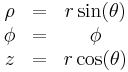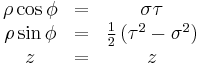Definition of coordinates	$\begin{matrix} r & = & \sqrt{x^2%2By^2%2Bz^2} \\ \theta & = & \arccos(z/r)\\ \phi & = & \arctan(y/x) \\ \end{matrix}$	$\begin{matrix} r & = & \sqrt{\rho^2 %2B z^2} \\ \theta & = & \arctan{(\rho/z)}\\ \phi & = & \phi \end{matrix}$	$\begin{matrix} \rho & = & r\sin(\theta) \\ \phi & = & \phi\\ z & = & r\cos(\theta) \end{matrix}$	$\begin{matrix} \rho\cos\phi & = & \sigma \tau\\ \rho\sin\phi & = & \frac{1}{2} \left( \tau^{2} - \sigma^{2} \right) \\ z & = & z \end{matrix}$
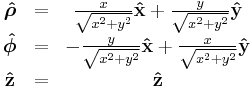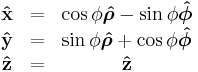Definition of unit vectors	$\begin{matrix} \boldsymbol{\hat \rho} & = & \frac{x}{\sqrt{x^2%2By^2}}\mathbf{\hat x}%2B\frac{y}{\sqrt{x^2%2By^2}}\mathbf{\hat y} \\ \boldsymbol{\hat\phi} & = & -\frac{y}{\sqrt{x^2%2By^2}}\mathbf{\hat x}%2B\frac{x}{\sqrt{x^2%2By^2}}\mathbf{\hat y} \\ \mathbf{\hat z} & = & \mathbf{\hat z} \end{matrix}$	$\begin{matrix} \mathbf{\hat x} & = & \cos\phi\boldsymbol{\hat \rho}-\sin\phi\boldsymbol{\hat\phi} \\ \mathbf{\hat y} & = & \sin\phi\boldsymbol{\hat \rho}%2B\cos\phi\boldsymbol{\hat\phi} \\ \mathbf{\hat z} & = & \mathbf{\hat z} \end{matrix}$	$\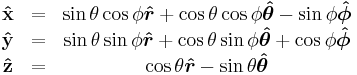begin{matrix} \mathbf{\hat x} & = & \sin\theta\cos\phi\boldsymbol{\hat r}%2B\cos\theta\cos\phi\boldsymbol{\hat\theta}-\sin\phi\boldsymbol{\hat\phi} \\ \mathbf{\hat y} & = & \sin\theta\sin\phi\boldsymbol{\hat r}%2B\cos\theta\sin\phi\boldsymbol{\hat\theta}%2B\cos\phi\boldsymbol{\hat\phi} \\ \mathbf{\hat z} & = & \cos\theta \boldsymbol{\hat r}-\sin\theta \boldsymbol{\hat\theta} \\ \end{matrix}$	$\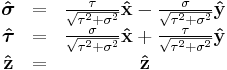begin{matrix} \boldsymbol{\hat \sigma} & = & \frac{\tau}{\sqrt{\tau^2%2B\sigma^2}}\mathbf{\hat x}-\frac{\sigma}{\sqrt{\tau^2%2B\sigma^2}}\mathbf{\hat y} \\ \boldsymbol{\hat\tau} & = & \frac{\sigma}{\sqrt{\tau^2%2B\sigma^2}}\mathbf{\hat x}%2B\frac{\tau}{\sqrt{\tau^2%2B\sigma^2}}\mathbf{\hat y} \\ \mathbf{\hat z} & = & \mathbf{\hat z} \end{matrix}$
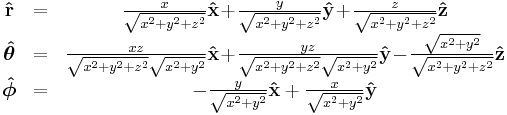Definition of unit vectors	$\begin{matrix} \mathbf{\hat r} &=& \frac{ x }{\sqrt{x^2%2By^2%2Bz^2}}\mathbf{\hat x}\!%2B\!\frac{ y }{\sqrt{x^2%2By^2%2Bz^2}}\mathbf{\hat y}\!%2B\!\frac{z}{\sqrt{x^2%2By^2%2Bz^2}}\mathbf{\hat z}\\ \boldsymbol{\hat\theta} &=& \frac{ xz }{\sqrt{x^2%2By^2%2Bz^2}\sqrt{x^2%2By^2}}\mathbf{\hat x}\!%2B\!\frac{ yz }{\sqrt{x^2%2By^2%2Bz^2}\sqrt{x^2%2By^2}}\mathbf{\hat y}\!-\!\frac{\sqrt{x^2%2By^2}}{\sqrt{x^2%2By^2%2Bz^2}}\mathbf{\hat z} \\ \boldsymbol{\hat\phi} &=& -\frac{y}{\sqrt{x^2%2By^2}}\mathbf{\hat x}%2B\frac{x}{\sqrt{x^2%2By^2}}\mathbf{\hat y} \end{matrix}$	$\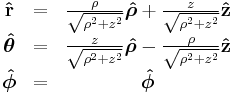begin{matrix} \mathbf{\hat r} & = & \frac{\rho}{\sqrt{\rho^2 %2Bz^2}}\boldsymbol{\hat \rho}%2B\frac{ z}{\sqrt{\rho^2 %2Bz^2}}\mathbf{\hat z} \\ \boldsymbol{\hat\theta} & = & \frac{z }{\sqrt{\rho^2 %2Bz^2}}\boldsymbol{\hat \rho}-\frac{\rho}{\sqrt{\rho^2 %2Bz^2}}\mathbf{\hat z} \\ \boldsymbol{\hat\phi} & = & \boldsymbol{\hat\phi} \end{matrix}$	$\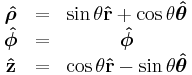begin{matrix} \boldsymbol{\hat \rho} & = & \sin\theta\mathbf{\hat r}%2B\cos\theta\boldsymbol{\hat\theta} \\ \boldsymbol{\hat\phi} & = & \boldsymbol{\hat\phi} \\ \mathbf{\hat z} & = & \cos\theta\mathbf{\hat r}-\sin\theta\boldsymbol{\hat\theta} \\ \end{matrix}$	$\begin{matrix} \end{matrix}$
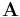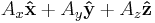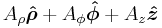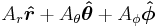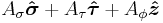A vector field $\mathbf{A}$	$A_x\mathbf{\hat x} %2B A_y\mathbf{\hat y} %2B A_z\mathbf{\hat z}$	$A_\rho\boldsymbol{\hat \rho} %2B A_\phi\boldsymbol{\hat \phi} %2B A_z\boldsymbol{\hat z}$	$A_r\boldsymbol{\hat r} %2B A_\theta\boldsymbol{\hat \theta} %2B A_\phi\boldsymbol{\hat \phi}$	$A_\sigma\boldsymbol{\hat \sigma} %2B A_\tau\boldsymbol{\hat \tau} %2B A_\phi\boldsymbol{\hat z}$
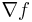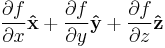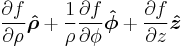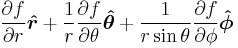Gradient $\nabla f$	${\partial f \over \partial x}\mathbf{\hat x} %2B {\partial f \over \partial y}\mathbf{\hat y} %2B {\partial f \over \partial z}\mathbf{\hat z}$	${\partial f \over \partial \rho}\boldsymbol{\hat \rho} %2B {1 \over \rho}{\partial f \over \partial \phi}\boldsymbol{\hat \phi} %2B {\partial f \over \partial z}\boldsymbol{\hat z}$	${\partial f \over \partial r}\boldsymbol{\hat r} %2B {1 \over r}{\partial f \over \partial \theta}\boldsymbol{\hat \theta} %2B {1 \over r\sin\theta}{\partial f \over \partial \phi}\boldsymbol{\hat \phi}$	$\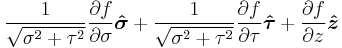frac{1}{\sqrt{\sigma^{2} %2B \tau^{2}}} {\partial f \over \partial \sigma}\boldsymbol{\hat \sigma} %2B \frac{1}{\sqrt{\sigma^{2} %2B \tau^{2}}} {\partial f \over \partial \tau}\boldsymbol{\hat \tau} %2B {\partial f \over \partial z}\boldsymbol{\hat z}$
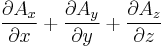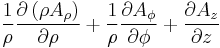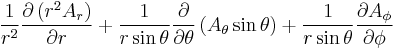Divergence $\nabla \cdot \mathbf{A}$	${\partial A_x \over \partial x} %2B {\partial A_y \over \partial y} %2B {\partial A_z \over \partial z}$	${1 \over \rho}{\partial \left( \rho A_\rho \right) \over \partial \rho} %2B {1 \over \rho}{\partial A_\phi \over \partial \phi} %2B {\partial A_z \over \partial z}$	${1 \over r^2}{\partial \left( r^2 A_r \right) \over \partial r} %2B {1 \over r\sin\theta}{\partial \over \partial \theta} \left( A_\theta\sin\theta \right) %2B {1 \over r\sin\theta}{\partial A_\phi \over \partial \phi}$	$\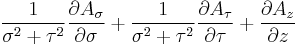frac{1}{\sigma^{2} %2B \tau^{2}}{\partial A_\sigma \over \partial \sigma} %2B \frac{1}{\sigma^{2} %2B \tau^{2}}{\partial A_\tau \over \partial \tau} %2B {\partial A_z \over \partial z}$
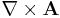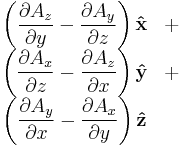Curl $\nabla \times \mathbf{A}$	$\begin{matrix} \displaystyle\left({\partial A_z \over \partial y} - {\partial A_y \over \partial z}\right) \mathbf{\hat x} & %2B \\ \displaystyle\left({\partial A_x \over \partial z} - {\partial A_z \over \partial x}\right) \mathbf{\hat y} & %2B \\ \displaystyle\left({\partial A_y \over \partial x} - {\partial A_x \over \partial y}\right) \mathbf{\hat z} & \ \end{matrix}$	$\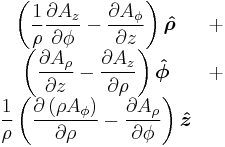begin{matrix} \displaystyle\left({1 \over \rho}{\partial A_z \over \partial \phi} - {\partial A_\phi \over \partial z}\right) \boldsymbol{\hat \rho} & %2B \\ \displaystyle\left({\partial A_\rho \over \partial z} - {\partial A_z \over \partial \rho}\right) \boldsymbol{\hat \phi} & %2B \\ \displaystyle{1 \over \rho}\left({\partial \left( \rho A_\phi \right) \over \partial \rho} - {\partial A_\rho \over \partial \phi}\right) \boldsymbol{\hat z} & \ \end{matrix}$	$\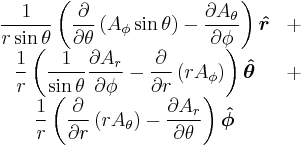begin{matrix} \displaystyle{1 \over r\sin\theta}\left({\partial \over \partial \theta} \left( A_\phi\sin\theta \right) - {\partial A_\theta \over \partial \phi}\right) \boldsymbol{\hat r} & %2B \\ \displaystyle{1 \over r}\left({1 \over \sin\theta}{\partial A_r \over \partial \phi} - {\partial \over \partial r} \left( r A_\phi \right) \right) \boldsymbol{\hat \theta} & %2B \\ \displaystyle{1 \over r}\left({\partial \over \partial r} \left( r A_\theta \right) - {\partial A_r \over \partial \theta}\right) \boldsymbol{\hat \phi} & \ \end{matrix}$	$\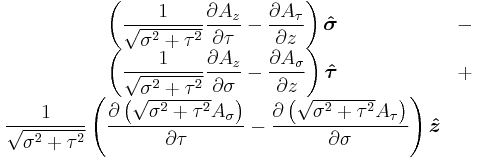begin{matrix} \displaystyle\left(\frac{1}{\sqrt{\sigma^{2} %2B \tau^{2}}}{\partial A_z \over \partial \tau} - {\partial A_\tau \over \partial z}\right) \boldsymbol{\hat \sigma} & - \\ \displaystyle\left(\frac{1}{\sqrt{\sigma^{2} %2B \tau^{2}}}{\partial A_z \over \partial \sigma}- {\partial A_\sigma \over \partial z}\right) \boldsymbol{\hat \tau} & %2B \\ \displaystyle\frac{1}{\sqrt{\sigma^{2} %2B \tau^{2}}}\left({\partial \left( \sqrt{\sigma^{2} %2B \tau^{2}} A_\sigma \right) \over \partial \tau} - {\partial \left( \sqrt{\sigma^{2} %2B \tau^{2}} A_\tau \right) \over \partial \sigma}\right) \boldsymbol{\hat z} & \ \end{matrix}$
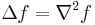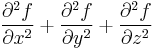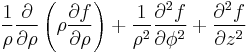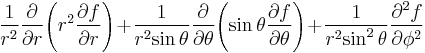Laplace operator $\Delta f = \nabla^2 f$	${\partial^2 f \over \partial x^2} %2B {\partial^2 f \over \partial y^2} %2B {\partial^2 f \over \partial z^2}$	${1 \over \rho}{\partial \over \partial \rho}\left(\rho {\partial f \over \partial \rho}\right) %2B {1 \over \rho^2}{\partial^2 f \over \partial \phi^2} %2B {\partial^2 f \over \partial z^2}$	${1 \over r^2}{\partial \over \partial r}\!\left(r^2 {\partial f \over \partial r}\right) \!%2B\!{1 \over r^2\!\sin\theta}{\partial \over \partial \theta}\!\left(\sin\theta {\partial f \over \partial \theta}\right) \!%2B\!{1 \over r^2\!\sin^2\theta}{\partial^2 f \over \partial \phi^2}$	$\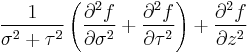frac{1}{\sigma^{2} %2B \tau^{2}} \left( \frac{\partial^{2} f}{\partial \sigma^{2}} %2B \frac{\partial^{2} f}{\partial \tau^{2}} \right) %2B \frac{\partial^{2} f}{\partial z^{2}}$
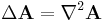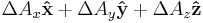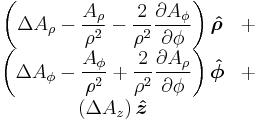Vector Laplacian $\Delta \mathbf{A} = \nabla^2 \mathbf{A}$	$\Delta A_x \mathbf{\hat x} %2B \Delta A_y \mathbf{\hat y} %2B \Delta A_z \mathbf{\hat z}$	$\begin{matrix} \displaystyle\left(\Delta A_\rho - {A_\rho \over \rho^2} - {2 \over \rho^2}{\partial A_\phi \over \partial \phi}\right) \boldsymbol{\hat \rho} & %2B \\ \displaystyle\left(\Delta A_\phi - {A_\phi \over \rho^2} %2B {2 \over \rho^2}{\partial A_\rho \over \partial \phi}\right) \boldsymbol{\hat\phi} & %2B \\ \displaystyle\left(\Delta A_z \right) \boldsymbol{\hat z} & \ \end{matrix}$	$\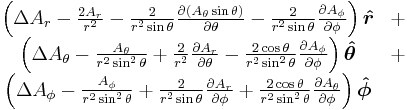begin{matrix} \left(\Delta A_r - {2 A_r \over r^2} - {2 \over r^2\sin\theta}{\partial \left(A_\theta \sin\theta\right) \over \partial\theta} - {2 \over r^2\sin\theta}{\partial A_\phi \over \partial \phi}\right) \boldsymbol{\hat r} & %2B \\ \left(\Delta A_\theta - {A_\theta \over r^2\sin^2\theta} %2B {2 \over r^2}{\partial A_r \over \partial \theta} - {2 \cos\theta \over r^2\sin^2\theta}{\partial A_\phi \over \partial \phi}\right) \boldsymbol{\hat\theta} & %2B \\ \left(\Delta A_\phi - {A_\phi \over r^2\sin^2\theta} %2B {2 \over r^2\sin\theta}{\partial A_r \over \partial \phi} %2B {2 \cos\theta \over r^2\sin^2\theta}{\partial A_\theta \over \partial \phi}\right) \boldsymbol{\hat\phi} & \end{matrix}$
Material derivative 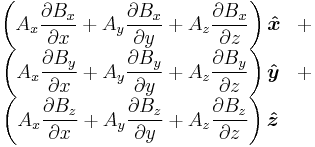^[1] $(\mathbf{A} \cdot \nabla) \mathbf{B}$	$\begin{matrix} \displaystyle\left(A_x \frac{\partial B_x}{\partial x}%2BA_y \frac{\partial B_x}{\partial y} %2B A_z \frac{\partial B_x}{\partial z}\right)\boldsymbol{\hat{x}} & %2B \\ \displaystyle\left(A_x \frac{\partial B_y}{\partial x}%2BA_y \frac{\partial B_y}{\partial y} %2B A_z \frac{\partial B_y}{\partial z}\right)\boldsymbol{\hat{y}} & %2B \\ \displaystyle\left(A_x \frac{\partial B_z}{\partial x}%2BA_y \frac{\partial B_z}{\partial y} %2B A_z \frac{\partial B_z}{\partial z}\right)\boldsymbol{\hat{z}} \end{matrix}$	$\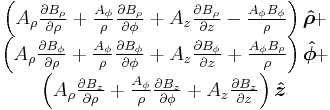begin{matrix} \left(A_\rho \frac{\partial B_\rho}{\partial \rho}%2B\frac{A_\phi}{\rho}\frac{\partial B_\rho}{\partial \phi}%2BA_z\frac{\partial B_\rho}{\partial z}-\frac{A_\phi B_\phi}{\rho}\right) \boldsymbol{\hat\rho} \!%2B\!\\ \left(A_\rho \frac{\partial B_\phi}{\partial \rho}%2B\frac{A_\phi}{\rho}\frac{\partial B_\phi}{\partial \phi}%2BA_z\frac{\partial B_\phi}{\partial z}%2B\frac{A_\phi B_\rho}{\rho}\right) \boldsymbol{\hat\phi}\!%2B\!\\ \left(A_\rho \frac{\partial B_z }{\partial \rho}%2B\frac{A_\phi}{\rho}\frac{\partial B_z }{\partial \phi}%2BA_z\frac{\partial B_z }{\partial z} \right) \boldsymbol{\hat z} \end{matrix}$	$\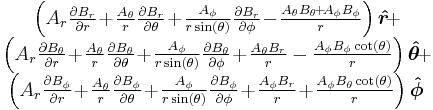begin{matrix} \left(A_r \frac{\partial B_r}{\partial r}\!%2B\!\frac{A_\theta}{r}\frac{\partial B_r}{\partial \theta}\!%2B\!\frac{A_\phi}{r\sin(\theta)}\frac{\partial B_r}{\partial \phi}\!-\!\frac{A_\theta B_\theta\!%2B\!A_\phi B_\phi}{r}\right) \boldsymbol{\hat r} \!%2B\!\\ \left(A_r \frac{\partial B_\theta}{\partial r}\!%2B\!\frac{A_\theta}{r}\frac{\partial B_\theta}{\partial \theta}\!%2B\!\frac{A_\phi}{r\sin(\theta)}\frac{\partial B_\theta}{\partial \phi}\!%2B\!\frac{A_\theta B_r}{r}-\frac{A_\phi B_\phi\cot(\theta)}{r}\right) \boldsymbol{\hat\theta} \!%2B\!\\ \left(A_r \frac{\partial B_\phi}{\partial r}\!%2B\!\frac{A_\theta}{r}\frac{\partial B_\phi}{\partial \theta}\!%2B\!\frac{A_\phi}{r\sin(\theta)}\frac{\partial B_\phi}{\partial \phi}\!%2B\!\frac{A_\phi B_r}{r}\!%2B\!\frac{A_\phi B_\theta \cot(\theta)}{r}\right)\boldsymbol{\hat\phi} \end{matrix}$
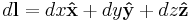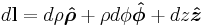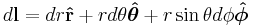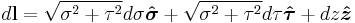Differential displacement	$d\mathbf{l} = dx\mathbf{\hat x} %2B dy\mathbf{\hat y} %2B dz\mathbf{\hat z}$	$d\mathbf{l} = d\rho\boldsymbol{\hat \rho} %2B \rho d\phi\boldsymbol{\hat \phi} %2B dz\boldsymbol{\hat z}$	$d\mathbf{l} = dr\mathbf{\hat r} %2B rd\theta\boldsymbol{\hat \theta} %2B r\sin\theta d\phi\boldsymbol{\hat \phi}$	$d\mathbf{l} = \sqrt{\sigma^{2} %2B \tau^{2}} d\sigma\boldsymbol{\hat \sigma} %2B \sqrt{\sigma^{2} %2B \tau^{2}} d\tau\boldsymbol{\hat \tau} %2B dz\boldsymbol{\hat z}$
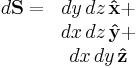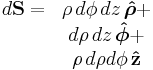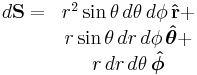Differential normal area	$\begin{matrix}d\mathbf{S} = &dy\,dz\,\mathbf{\hat x} %2B \\ &dx\,dz\,\mathbf{\hat y} %2B \\ &dx\,dy\,\mathbf{\hat z}\end{matrix}$	$\begin{matrix} d\mathbf{S} = & \rho\, d\phi\, dz\,\boldsymbol{\hat \rho} %2B \\ & d\rho \,dz\,\boldsymbol{\hat \phi} %2B \\ & \rho \,d\rho d\phi \,\mathbf{\hat z} \end{matrix}$	$\begin{matrix} d\mathbf{S} = & r^2 \sin\theta \,d\theta \,d\phi \,\mathbf{\hat r} %2B \\ & r\sin\theta \,dr\,d\phi \,\boldsymbol{\hat \theta} %2B \\ & r\,dr\,d\theta\,\boldsymbol{\hat \phi} \end{matrix}$	$\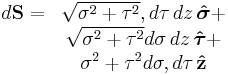begin{matrix} d\mathbf{S} = & \sqrt{\sigma^{2} %2B \tau^{2}}, d\tau\, dz\,\boldsymbol{\hat \sigma} %2B \\ & \sqrt{\sigma^{2} %2B \tau^{2}} d\sigma\,dz\,\boldsymbol{\hat \tau} %2B \\ & \sigma^{2} %2B \tau^{2} d\sigma, d\tau \,\mathbf{\hat z} \end{matrix}$
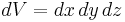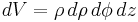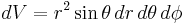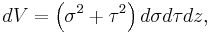Differential volume	$dV = dx\,dy\,dz \,$	$dV = \rho\, d\rho\, d\phi\, dz\,$	$dV = r^2\sin\theta \,dr\,d\theta\, d\phi\,$	$dV = \left( \sigma^{2} %2B \tau^{2} \right) d\sigma d\tau dz,$
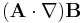
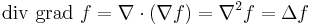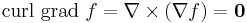
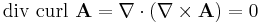
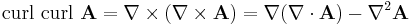Non-trivial calculation rules: $\operatorname{div\ grad\ } f = \nabla \cdot (\nabla f) = \nabla^2 f = \Delta f$ (Laplacian) $\operatorname{curl\ grad\ } f = \nabla \times (\nabla f) = \mathbf{0}$ $\operatorname{div\ curl\ } \mathbf{A} = \nabla \cdot (\nabla \times \mathbf{A}) = 0$ $\operatorname{curl\ curl\ } \mathbf{A} = \nabla \times (\nabla \times \mathbf{A}) = \nabla (\nabla \cdot \mathbf{A}) - \nabla^2 \mathbf{A}$ (using Lagrange's formula for the cross product) $\Delta f g = f \Delta g %2B 2 \nabla f \cdot \nabla g %2B g \Delta f$